Additiv syntese
Klassisk additiv syntese baseres på ideen om, at komplekse bølgeformer og dermed interessante klange kan fremstilles (approksimativt) ved ganske enkelt at sammenlægge en række sinusbølger, som svinger ved forskellige frekvenser og amplituder. Den matematiske ide bag dette findes i teorien om Fourierrækker.
Standardbølgeformer
Som eksempel på additiv syntese kan vi starte med at generere tre standardbølgeformer. Kilden til algoritmerne er Thor Magnussons (2021)1 udmærkede introduktion til additiv syntese. Sørg for at visualisere lydserverens output.
Disse bølgeformer udnytter den såkaldt naturlige overtonerække, som består af en række overtoner med frekvenser, der ligger et helt antal gange over en grundtones frekvens. Hvis grundtonen svinger ved 100 Hz, vil den første tone i den naturlige overtonerække svinge ved 200 Hz, den næste ved 300 Hz, derefter 400 Hz og så fremdeles.
Savtakket bølgeform
Den savtakkede bølgeform indeholder alle overtoner i overtonerækken. Her blot de første 30 overtoner.
{
var sig = 30.collect({
arg num;
var overtone = num + 1;
SinOsc.ar(220 * overtone) * 0.5 / overtone;
});
sig.sum * 0.1;
}.play;
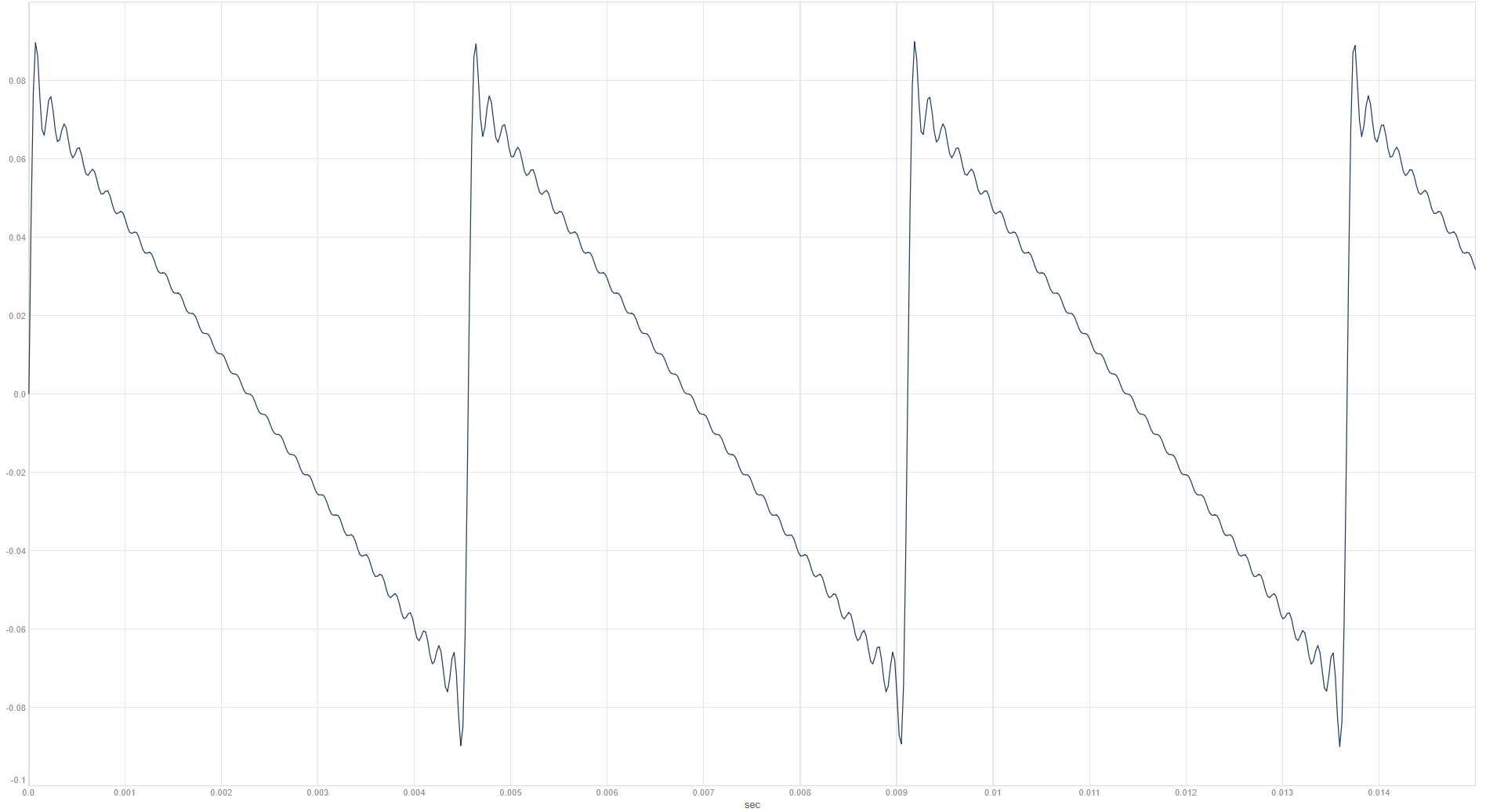
Bemærk på spektrogrammet, at overtonerne stopper brat ved cirka 30 * 220 Hz = 6,6 kHz.
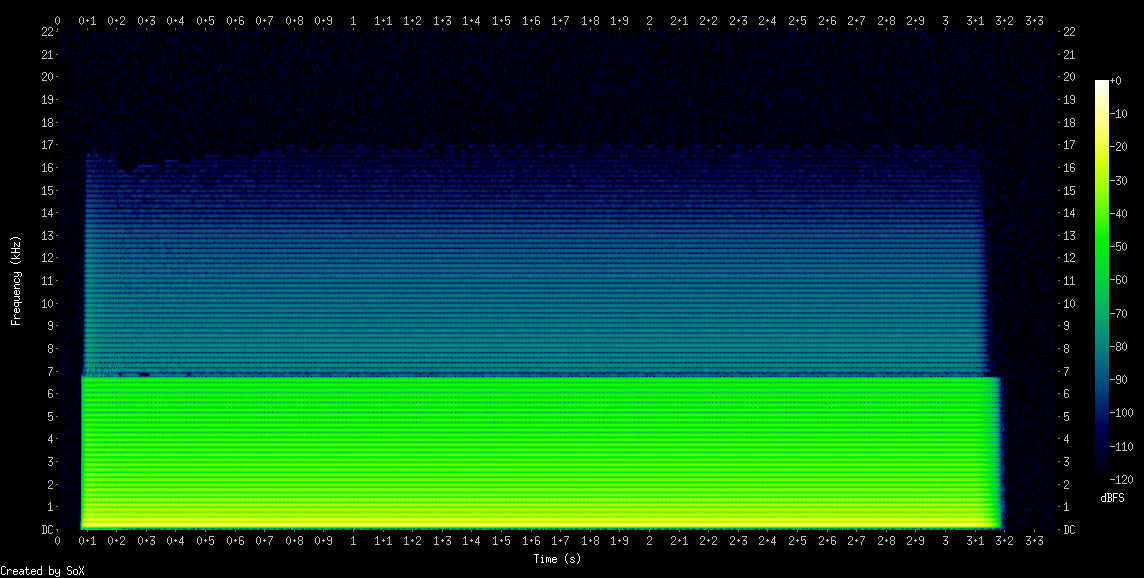
Firkantet bølgeform
Den firkantede bølgeform kan skabes med overtonerne med ulige numre, dvs. nr. 1 (grundtonen), nr. 3, nr. 5, nr. 7 osv. Overtonerne falder i amplitude, jo højere vi kommer op. Her blot de første 30 overtoner.
{
var sig = 30.collect({
arg num;
var overtone = num * 2 + 1;
SinOsc.ar(220 * overtone) * 0.5 / overtone;
});
sig.sum * 0.1;
}.play;
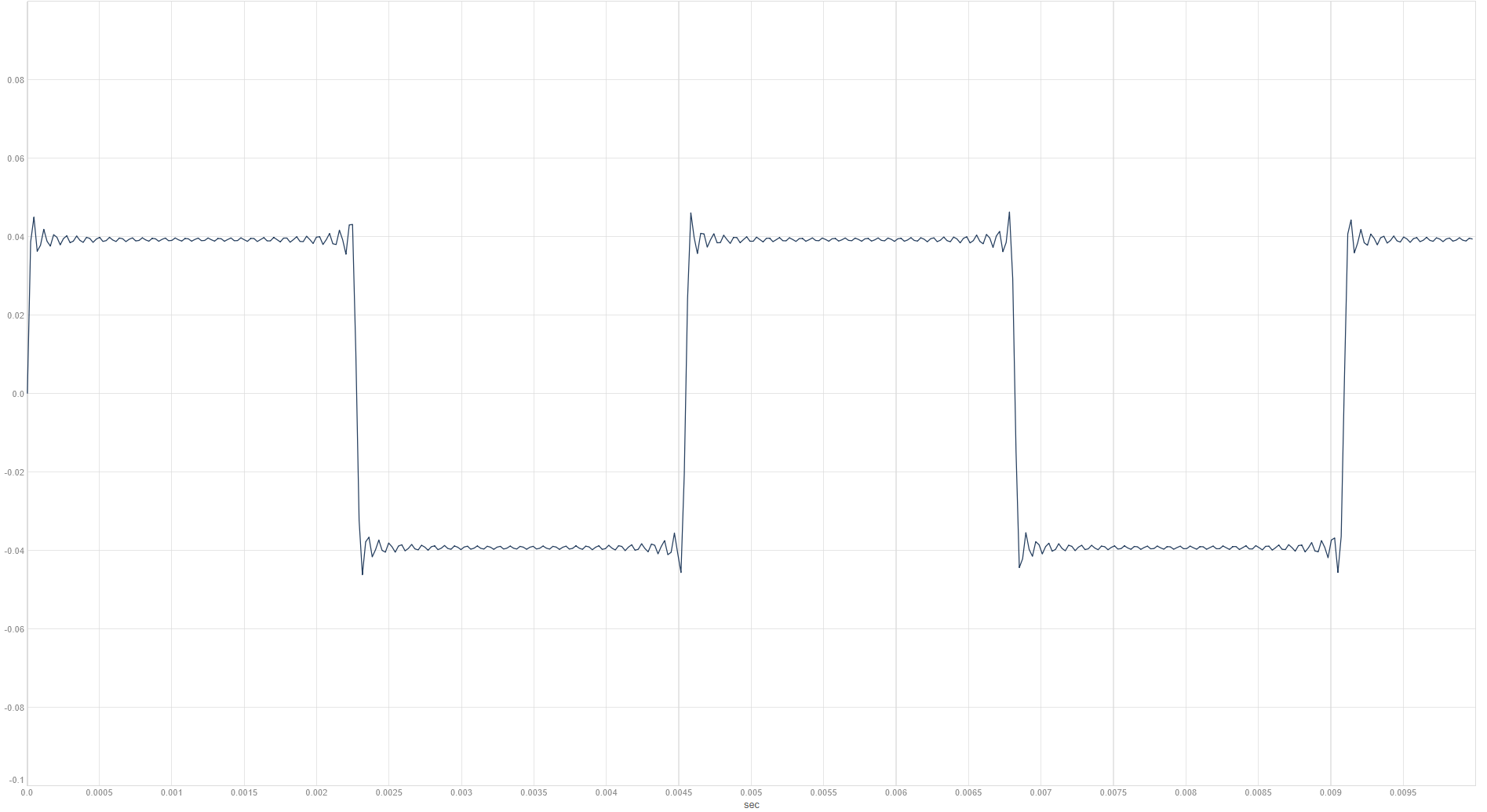
Bemærk på spektrogrammet, hvordan der er større afstand mellem overtonerne end ved den savtakkede bølgeform ovenfor.
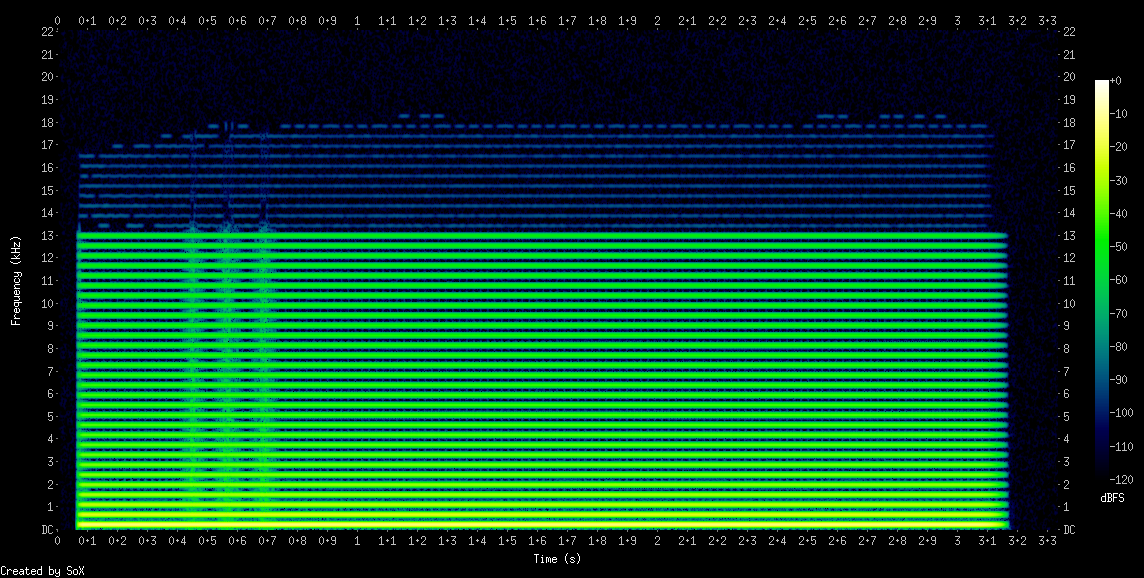
Trekantet bølgeform
Den trekantede bølgeform kan ligesom den firkantede skabes med overtonerne med ulige numre, dvs. nr. 1 grundtonen, nr. 3, nr. 5, nr. 7 osv. Overtonerne falder i amplitude, jo højere vi kommer op, men med en lidt anden formel end ved den firkantede. Her blot de første 30 overtoner.
{
var sig = 30.collect({
arg num;
var overtone = num * 2 + 1;
SinOsc.ar(440 * overtone, pi/2) * 0.7 / overtone.pow(2);
});
sig.sum * 0.1;
}.play;
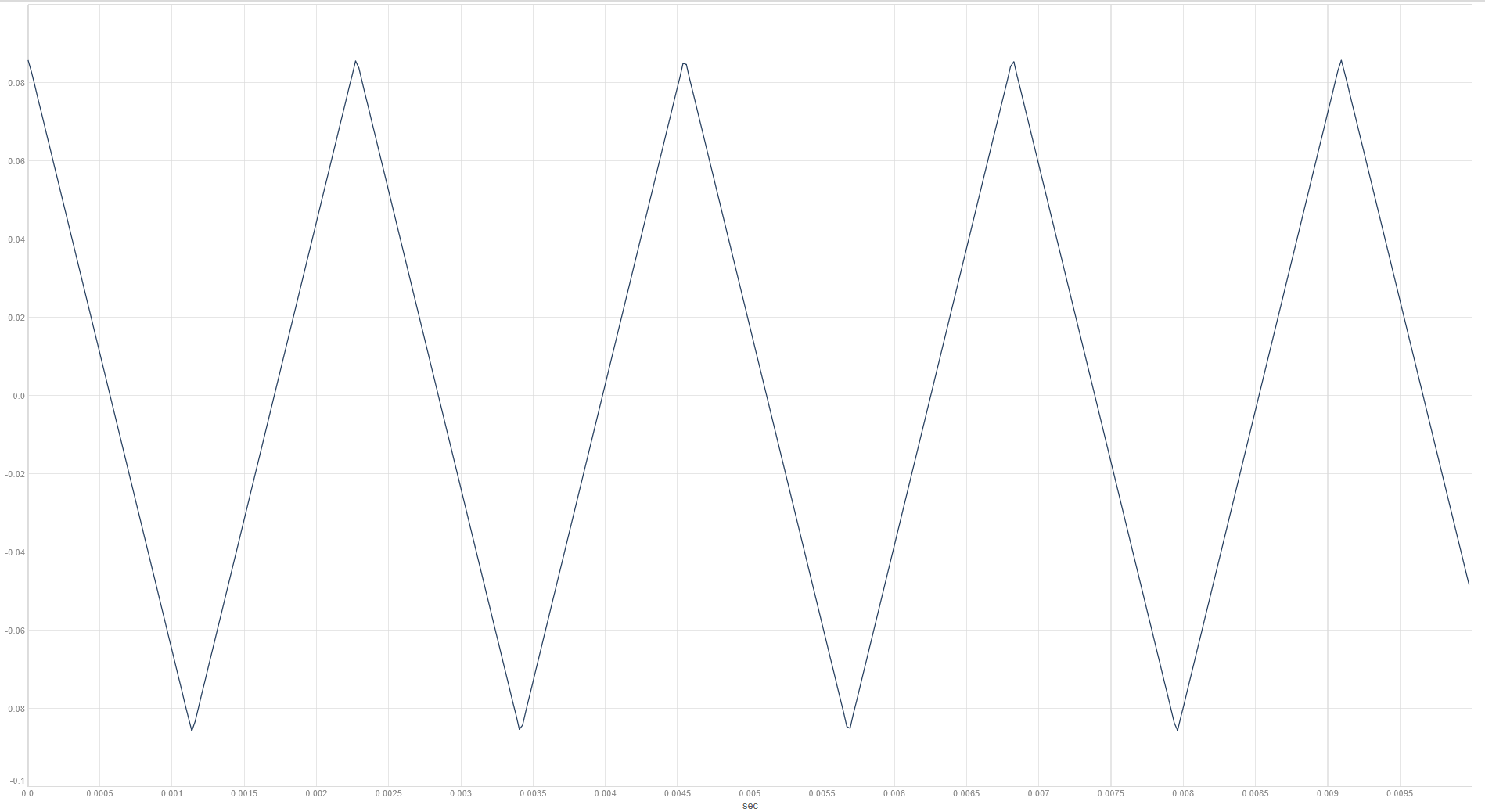
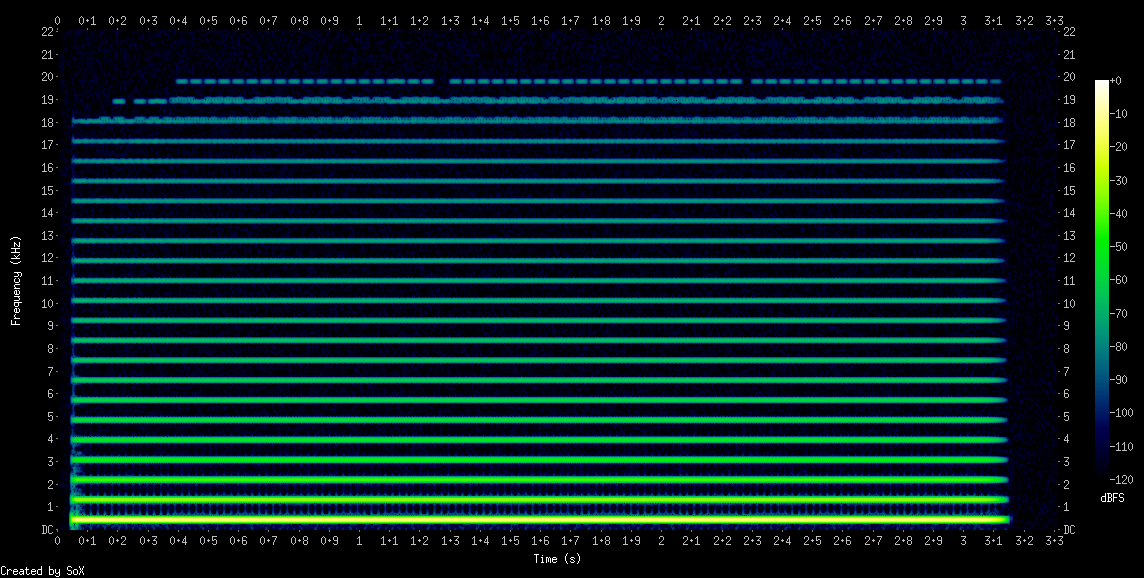
Bemærk på spektrogrammet, hvordan der er endnu større afstand mellem overtonerne end ved den savtakkede og den firkantede bølgeform ovenfor.
Andre eksempler
Man behøver naturligvis ikke begrænse sig til standardbølgeformer eller for den sags skyld den naturlige overtonerække.
En ikke-standard bølgeform
Her er eksempelvis en ikke-standard bølgeform, som består af hver tredje overtone.
{
var sig = 15.collect({
arg num;
var overtone = num * 3 + 1;
SinOsc.ar(220 * overtone) * 0.6 / overtone
});
sig * 0.1;
}.play;
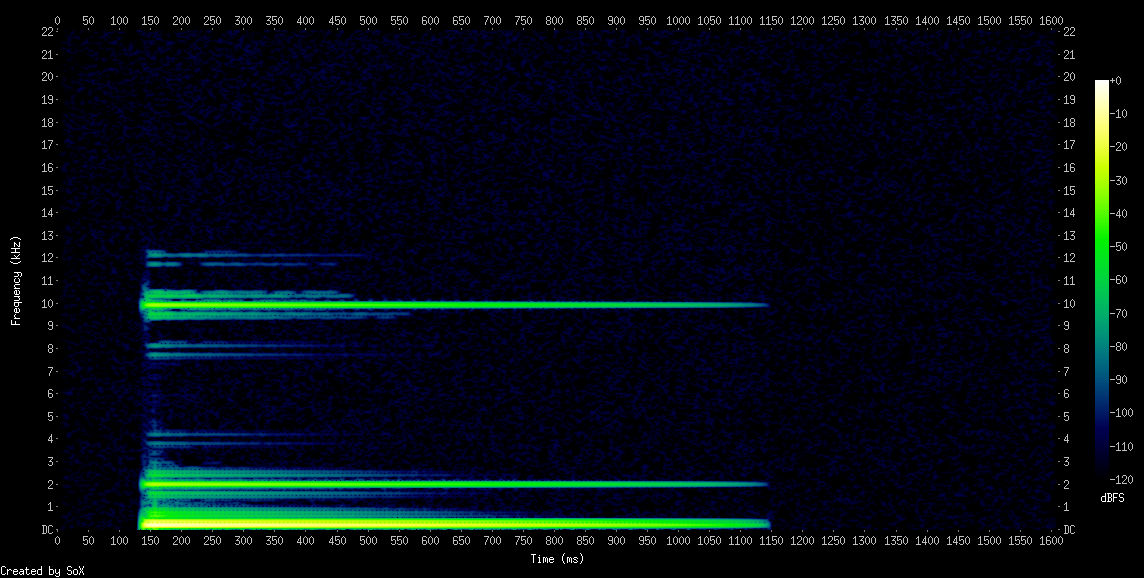
En klokkelyd
Dette eksempel på en klokkelyd er løseligt baseret på et eksempel fra Curtis Roads (2023, p. 123)2. Lyden indeholder følgende sinustoner:
- En grundtone, som klinger ved 200 Hz.
- En overtone, som klinger ved 2000 Hz.
- To partialtoner (dvs. ikke-harmoniske overtoner), som klinger ved henholdsvis 347,5 Hz og 9921,8 Hz.
{
var freqs = [200, 347.5, 2000, 9921.8];
var amplitudes = [0.73, 0.18, 0.05, 0.04];
var sig = SinOsc.ar(freqs) * amplitudes;
var env = EnvGen.kr(Env.perc, doneAction: Done.freeSelf);
sig = sig.sum;
sig.dup * env * 0.1;
}.play;
En mere kaotisk klokkelyd
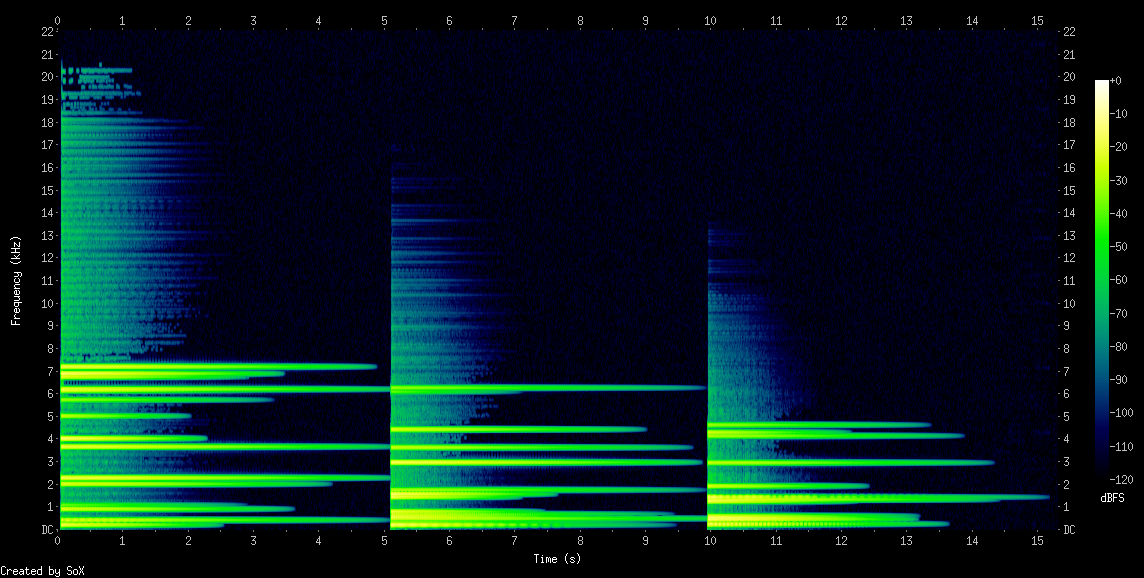
Klokkelyde er generelt kendetegnet ved et højt indhold af partialtoner. For at skabe unikke lyde kan vi give hver partialtone en tilfældig frekvens, amplitude og envelope. Dertil udnytter vi de to generatorer Rand og ExpRand, som genererer en tilfældig værdi mellem et minimum og et maksimum, når Synth'en startes. Da vi ikke har én envelope, som styrer lydstyrken, kan vi heller ikke vide hvilken af de 16 envelopes, der skal afslutte Synth'en med doneAction. Derfor anvender vi en særlig UGen kalder DetectSilence, som kan stoppe Synth'en, når den har detekteret stilhed i et givet tidsrum.
Kør blokken flere gange for at høre variationsmulighederne. Bemærk hvor længe de forskellige partialtoner klinger på grund af forskellige længder af release-segmenter.
Se i øvrigt også afsnittet om Rissets klokke.
{
var sig = 16.collect({
var freq = ExpRand(200, 8000);
var amp = ExpRand(0.05, 0.8);
var release = Rand(2, 6);
var env = EnvGen.kr(Env.perc(0.01, release));
SinOsc.ar(freq) * amp * env;
});
sig = sig.sum;
DetectSilence.ar(sig, doneAction: Done.freeSelf);
sig.dup * 0.1;
}.play;
Bemærk på spektrogrammet, hvordan de forskellige partialtoner klinger ud på forskellige tidspunkter.
-
Magnusson, T. (2021). Scoring Sound: Creative Music Coding with SuperCollider. In Leanpub. https://leanpub.com/ScoringSound ↩
-
Roads, C. (2023). The Computer Music Tutorial (2. ed.). MIT Press. ↩